Rabitz Lab Creates Tools to Define System Uncertainty
Suppose you’re asking a complex question in which a host of factors, or inputs, could contribute to the answer. In such a circumstance, each of the inputs will influence the certainty of your output answer to a varying degree.
These factors could arise in almost any system that defies easy analysis: the impact of design quirks on the safety of nuclear reactors, or the price of gas and its relation to climate policy, even something as prosaic as the factors that influence a healthy lifestyle.
But which inputs in such multivariate systems influence the certainty of the outcome, and what is the degree of that influence?
In short, can any of this be reliably quantified?
John Barr, a fifth-year graduate student in the Rabitz Lab and an applied mathematician, answers that question in the affirmative in a new paper out this week in The Society of Industrial and Applied Mathematics/American Statistical Association Journal on Uncertainty Quantification (SIAM/ASA JUQ).

Graduate student John Barr has created broadly applicable tools for interpreting data in complex input-output systems.
This investigation could be transformative for researchers by helping them determine how variations to inputs in experimental setups or computational models influence the outputs, which defines the subject of Sensitivity Analysis (SA).
Sensitivity Analysis has been a means of investigation for years, but Barr’s advance is expected to take it in new directions. Whether they work in health, engineering or economics, researchers who want to do a quantitative analysis of input-output relations may find this advance opens a wider door to the kinds of problems that can be examined through the SA lens.
In developing the methodology, Barr borrowed from something called kernel theory, which is pervasive in modern mathematical analysis but has not previously been adapted to the complex problems of SA. The porting-over of kernel theory to SA is at the heart of Barr’s innovation. In SA, a prime challenge is to understand the relationships between the inputs and outputs, and their connections. Kernel theory provides the means to compare the dependence between and within these classes of variables.
“In virtually any problem today there typically can be many, many variables. And, a fundamental question is, how do these variables work independently or together?” said Herschel Rabitz, the Charles Phelps Smyth ’16 *17 Professor of Chemistry. “It could be proteins as variables controlling the virus replication rate in a cell. It could be the pixels in a laser pulse shaper. It could be the keys on a piano and how you play them together or separately such that they combine to make a sound that is melodic.
“John had his own completely different approach to looking at SA, and it’s going to open up new classes of applications that were not accessible before,” Rabitz added. “It will allow us to look at complex problems – particularly biological problems – as multivariate systems in a new way. How do the variables interact? That’s always one of the biggest questions. All of the circumstances in any system share a common SA mathematical foundation, which can be addressed in a generalized way as laid out by John’s mathematical tools.”
Barr’s research, A Generalized Kernel Method for Global Sensitivity Analysis, was published in the journal this week. A second paper, including a more advanced algorithm, will be made public at a later date.
“Now that the basic tools and an increased efficiency have been reached, what’s exciting to me will be to see it applied to as diverse a class of problems as possible,” said Barr.
PROBABILITY DISTRIBUTION
Scientists often base a system’s complexity on the number of variables that are involved. For example, the basic model used by Barr for this research has around 90 inputs and about 50 outputs, a system of intermediate complexity. A really complex decision system could have thousands of inputs and outputs.
Trying to build probability distributions that capture the variable relationships in these complex systems is a challenge because of the sheer amount of data.
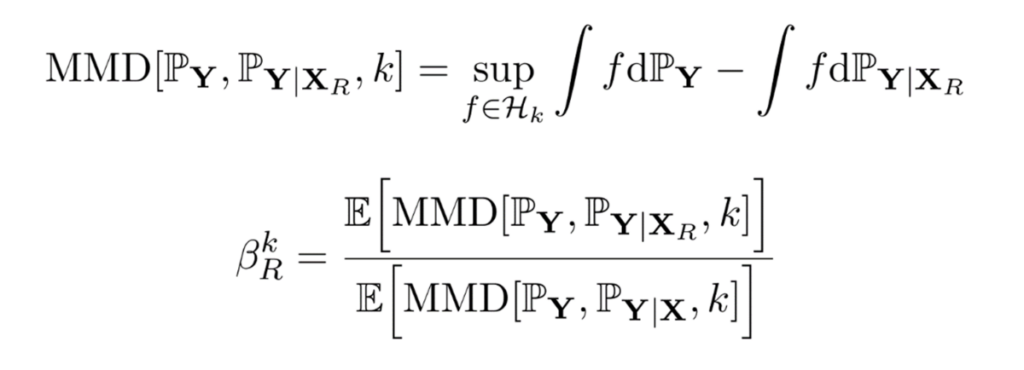
An example of the equation governing how kernels can be utilized to measure the sensitivity of the distribution of outputs with respect to the inputs.
Around the late aughts, researchers started doing work in probability theory to assess how to use statistical testing for these complex systems. One of them was Arthur Gretton, now a professor at University College London, who came up with a technique for expressing probability distributions with a new mathematical procedure. His research allowed scientists to project data from these complex systems into spaces where the calculations become significantly more manageable, even easy.
Barr zeroed in on the techniques for input-output applications, applying them to SA to come up with a whole new way of studying these systems. His work aims to reveal the nature of the many, variable probability distributions.
“Suppose that you have an input-output system and you could either simulate it or collect laboratory data, and then a distribution for the outputs will be produced,” said Barr. “And, another distribution would apply to the inputs. That’s what we study as our foundational cases – if you’re collecting information, then what features do the probability distributions have?
“We may ultimately find the inputs that aren’t that influential or don’t cause much change in the outputs, as well as identify the important ones that cause a lot of change in the outputs. The detailed mathematical tools provide a new perspective on such analyses.”
Barr created a rigorous mathematical proof that encompasses this goal for nearly any system with inputs and outputs. The proof is based upon various mathematical analyses that have been researched over the past half-century and relies on drawing them together.
“One of the attractive features about the method we’re proposing is that we show it can work for very general systems,” said Barr. “It really is the culmination of mathematics that has been developed by many others over a period of years that drives the new formulation of SA.
Read the full paper journal paper.
“A Generalized Kernel Method for Global Sensitivity Analysis,” was funded in part by the National Science Foundation (under grant CHE-1763198); the Princeton Program in Plasma Sciences and Technology; the Department of Energy (under grant DE-FG02-02EF15344) and the Army Research Office (under grant W911NF-19-1-0382).
