Torquato Lab: On Finding Hidden Order in Irregular Tilings
Conventional techniques of directing light or electrons through a material exploit the material’s regular, ordered structure to constrain the trajectory of the signal. But imagine if we could guide photons or electrons through an amorphous metamaterial in any direction of one’s choosing by exploiting the metamaterial’s irregular structure. Or what if we could better understand the formation of nanostructures in butterfly wings, or how the retinae of birds achieve their amazing uniformity or if we could more precisely control the self-assembly of nanoparticles?
How are these questions related? They can all be seen as certain optimizations of cellular structures, often of tile-like divisions of space, where the cells have certain optimal geometrical properties.
Resolving applied and theoretical questions like these are potential future impacts of a recent study in a collaboration of Professor Salvatore Torquato, the Lewis Bernard Professor of Natural Sciences and Professor of Chemistry at Princeton with colleagues from Australia, Germany, and Croatia, a project which analyzes a model for amorphous cellular structures aiming for an optimal ‘quantization of space’. By studying the so-called Quantizer problem, the researchers sought to better understand the formation of hidden order in disordered tessellations.

Photo by C. Todd Reichart
Their paper, “Universal hidden order in amorphous cellular geometries,” published last month in Nature Communications, investigates an iterative optimization of each single cell in the amorphous cellular systems that makes them more regular but retains both their global and local amorphousness. Surprisingly, independent of basically whatever the initial disorder is, the procedure converges to the same statistically indistinguishable spatial structures, and it drives the system towards an anomalous suppression of long-range density fluctuations, known as hyperuniformity.
Hyperuniformity is a concept that Torquato and colleague Frank Stillinger first defined in 2003. An intuitive picture of the rigorous theoretical concept can be given as follows: A random distribution of points inevitably leads to bunching and gaps among points both as you zoom-in and -out while viewing the point pattern. With a hyperuniform distribution of points, as you zoom-out the bunching and gaps diminish, and the distribution looks much less messy than a garden variety random distribution, rather more like a crystal—but not a crystal!
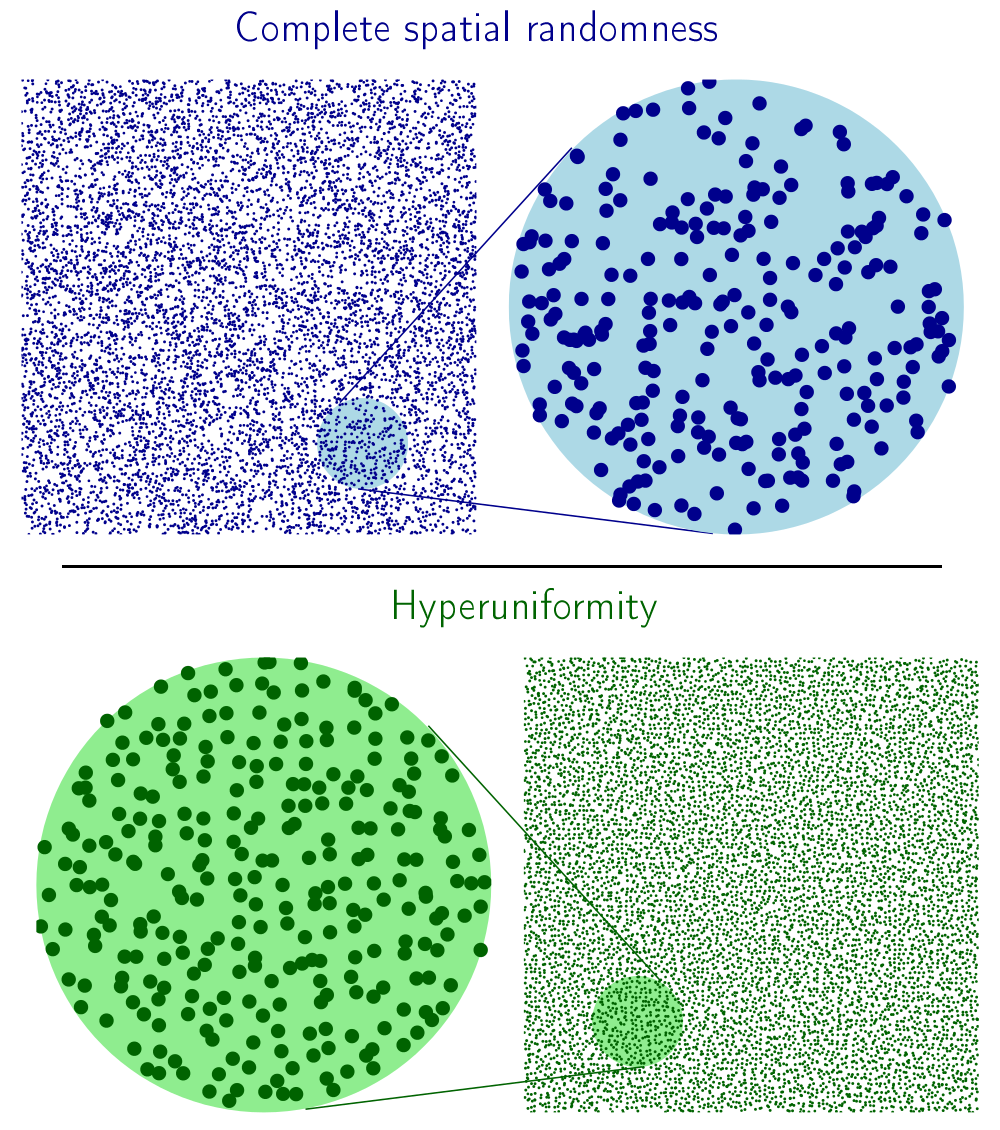
Diagram courtesy of the authors
Since the recent project is less focused on direct application than on fundamental implications, it can seem to reside in the world of the abstract. Torquato, Director of the Center for Complex Materials, offers this analogy: “Imagine beginning with a tessellation or tiling of space—like tiles in a bathroom, but with a twist—the tiles are irregularly shaped. We then systematically evolve the irregular tessellation via optimization techniques to study how the tessellation becomes more regular and hyperuniform during the evolutionary process.”
Michael Klatt, a postdoctoral researcher and first author of the paper, describes how by assigning a central point to each cell, each tessellation is related to a point pattern. That point pattern can be thought of as representing molecules in a liquid, trees in a forest, grains in a granular packing, galaxies in the universe, or nodes in telecommunication networks. He explains further, “In stochastic geometry, we are interested in the global configuration of the points rather than on what they shall represent.”
The numerical study uses optimization techniques from computer science as well as from mathematics and physics. “What I like about our research is that our methods and results are very straightforward. Take basically any amorphous point pattern. Now if each point moves just a little bit—optimal relative to its neighbors—and we do this again and again, we make the system not only globally uniform despite the local disorder, but we also
end up in statistically the same system no matter from which irregular point pattern we start,” Klatt says.
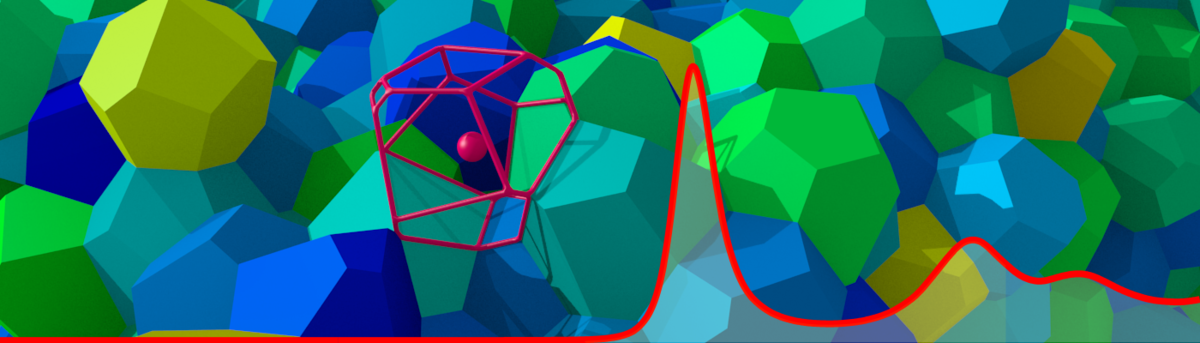
Image courtesy of the authors
“This is the most intriguing finding of our study,” he notes. “From whatever amorphous system we started, from highly uniform systems (stealthy hyperuniform) to extremely clustered and irregular patterns (anti hyperuniform), all of these systems very quickly became absolutely indistinguishable from one another, yet they remained fully amorphous.” Moreover, all of these systems quickly became effectively hyperuniform.
One of the goals of the project, then, was “to better understand disordered hyperuniform structures which are exotic and are shown to have novel physical properties,” says Torquato. The work contributes to the field by offering new insights into how ordered or disordered hyperuniform states of matter evolve by learning how to produce and generate randomness.
The project was truly interdisciplinary in nature as it applied techniques from physics to the mathematical model. The combination of theoretical and applied concepts, especially those from statistical physics and stochastic geometry, help to better understand how the iterative local optimization, known as Lloyd’s algorithm, leads to a global uniformity.

Video produced by Thomas Pigeon and Gerd Schröder-Turk.
The interplay between order and disorder is a common theme to many ongoing studies, and this work from Torquato’s group offers one new mechanism to better understand the concept. Further, it opens new questions which have already inspired some new interdisciplinary research projects in physics, mathematics, and materials science.
While Klatt is effusive when describing the research outcomes of the project and how it has the potential to spark follow-up studies by other scientists, he is similarly enthusiastic when recounting how collaborating on this project initiated the opportunity to bring him to Princeton.
When researchers are able to accurately model states of matter, this opens up the possibility for manipulating a plethora of physical properties, for example the propagation of waves, from light to seismic waves. Other potential applications may be found in the self-assembly of nanoparticles or arriving at a better understanding of cell biology.
Could these real-world systems share a universality similar to that found in the Quanitzer problem? Although the immediate novel contribution of this work may be its theoretical insights, its full significance may be well beyond the mathematical realm.
The paper, Universal hidden order in amorphous cellular geometries, by Michael A. Klatt, Jakov Lovrić, Duyu Chen, Sebastian C. Kapfer, Fabian M. Schaller, Philipp W. A. Schönhöfer, Bruce S. Gardiner, Ana-Sunčana Smith, Gerd E. Schröder-Turk and Salvatore Torquato was supported by the research group ‘Geometry and Physics of Spatial Random Systems’ funded by the German Science Foundation (DFG). Other funders include the European Research Council, the U.S. National Science Foundation and the KIT publication fund.
